[백준]3020: 개똥벌레(javascript)
https://www.acmicpc.net/problem/3020
3020번: 개똥벌레
개똥벌레 한 마리가 장애물(석순과 종유석)로 가득찬 동굴에 들어갔다. 동굴의 길이는 N미터이고, 높이는 H미터이다. (N은 짝수) 첫 번째 장애물은 항상 석순이고, 그 다음에는 종유석과 석순이
www.acmicpc.net
문제
개똥벌레 한 마리가 장애물(석순과 종유석)로 가득찬 동굴에 들어갔다. 동굴의 길이는 N미터이고, 높이는 H미터이다. (N은 짝수) 첫 번째 장애물은 항상 석순이고, 그 다음에는 종유석과 석순이 번갈아가면서 등장한다.
아래 그림은 길이가 14미터이고 높이가 5미터인 동굴이다. (예제 그림)

이 개똥벌레는 장애물을 피하지 않는다. 자신이 지나갈 구간을 정한 다음 일직선으로 지나가면서 만나는 모든 장애물을 파괴한다.
위의 그림에서 4번째 구간으로 개똥벌레가 날아간다면 파괴해야하는 장애물의 수는 총 여덟개이다. (4번째 구간은 길이가 3인 석순과 길이가 4인 석순의 중간지점을 말한다)
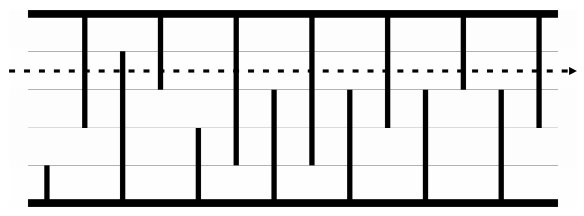
하지만, 첫 번째 구간이나 다섯 번째 구간으로 날아간다면 개똥벌레는 장애물 일곱개만 파괴하면 된다.
동굴의 크기와 높이, 모든 장애물의 크기가 주어진다. 이때, 개똥벌레가 파괴해야하는 장애물의 최솟값과 그러한 구간이 총 몇 개 있는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N과 H가 주어진다. N은 항상 짝수이다. (2 ≤ N ≤ 200,000, 2 ≤ H ≤ 500,000)
다음 N개 줄에는 장애물의 크기가 순서대로 주어진다. 장애물의 크기는 H보다 작은 양수이다.
출력
첫째 줄에 개똥벌레가 파괴해야 하는 장애물의 최솟값과 그러한 구간의 수를 공백으로 구분하여 출력한다.
예제 입력 1
6 7
1
5
3
3
5
1
예제 출력 1
2 3풀이
누적합 문제였습니다.
이해하기 쉬운 석순으로 이야기해보겠습니다.
첫번째 테스트케이스에서 석순은 1, 3, 5의 높이를 갖고있습니다. 최대 높이인 7짜리 배열을 만들어서
bottom = [0, 1, 0, 1, 0, 1, 0, 0] 이 됩니다. 가장 바닥이 index 1인 것을 생각하며
누적합으로 더하면
bottom = [3, 3, 2, 2, 1, 1, 0, 0] 이 됩니다.
같지만 순서만 반대로 종유석을 구해보겠습니다.
5, 3, 1의 높이를 갖고있으므로
top = [ 0, 0, 0, 1, 0, 1, 0, 1] 이 되어야합니다. (1번째 index가 바닥을 가리키게 하기 위해서)
이것을 누적합을 구하면
top = [0, 0, 0, 1, 2, 2, 3] 이 되는겁니다.
그래서 최종적으로 우리가 구하려는 종유석이 높이별로 몇개있는지 bottom + top을 통해 알 수 있습니다.
bottom + top = [3, 3, 2, 3, 2, 3, 2, 3] 이 됩니다.
이러면 2개만 부수면 되는게 총 3개가 되겠네요.
전체 코드
const fs = require("fs");
const filePath = process.platform === "linux" ? "/dev/stdin" : "input.txt";
const input = fs.readFileSync(filePath).toString().split("\n");
const [N, M] = input
.shift()
.split(" ")
.map((v) => parseInt(v));
//종유석
const bottom = Array.from({ length: M + 1 }, () => 0);
//석순
const top = Array.from({ length: M + 1 }, () => 0);
input.forEach((v, idx) => {
idx % 2 === 0 ? bottom[parseInt(v)]++ : top[M - parseInt(v) + 1]++;
});
for (let i = 1; i <= M; i++) {
top[i] += top[i - 1];
bottom[M - i] += bottom[M - i + 1];
}
let min = Infinity;
let cnt = 0;
for (let i = 1; i <= M; i++) {
if (top[i] + bottom[i] < min) {
cnt = 1;
min = top[i] + bottom[i];
} else if (top[i] + bottom[i] === min) {
cnt++;
}
}
console.log(min, cnt);