[프로그래머스]카드 짝 맞추기(java): 2021 KAKAO BLIND RECRUITMENT

https://programmers.co.kr/learn/courses/30/lessons/72415

코딩테스트 연습 - 카드 짝 맞추기

문제 설명

게임 개발자인 베로니는 개발 연습을 위해 다음과 같은 간단한 카드 짝맞추기 보드 게임을 개발해 보려고 합니다.
게임이 시작되면 화면에는 카드 16장이 뒷면을 위로하여 4 x 4 크기의 격자 형태로 표시되어 있습니다. 각 카드의 앞면에는 카카오프렌즈 캐릭터 그림이 그려져 있으며, 8가지의 캐릭터 그림이 그려진 카드가 각기 2장씩 화면에 무작위로 배치되어 있습니다.
유저가 카드를 2장 선택하여 앞면으로 뒤집었을 때 같은 그림이 그려진 카드면 해당 카드는 게임 화면에서 사라지며, 같은 그림이 아니라면 원래 상태로 뒷면이 보이도록 뒤집힙니다. 이와 같은 방법으로 모든 카드를 화면에서 사라지게 하면 게임이 종료됩니다.

게임에서 카드를 선택하는 방법은 다음과 같습니다.

• 카드는 커서를 이용해서 선택할 수 있습니다.
  • 커서는 4 x 4 화면에서 유저가 선택한 현재 위치를 표시하는 "굵고 빨간 테두리 상자"를 의미합니다.
• 커서는 [Ctrl] 키와 방향키에 의해 이동되며 키 조작법은 다음과 같습니다.
  • 방향키 ←, ↑, ↓, → 중 하나를 누르면, 커서가 누른 키 방향으로 1칸 이동합니다.
  • [Ctrl] 키를 누른 상태에서 방향키 ←, ↑, ↓, → 중 하나를 누르면, 누른 키 방향에 있는 가장 가까운 카드로 한번에 이동합니다.
    • 만약, 해당 방향에 카드가 하나도 없다면 그 방향의 가장 마지막 칸으로 이동합니다.
  • 만약, 누른 키 방향으로 이동 가능한 카드 또는 빈 공간이 없어 이동할 수 없다면 커서는 움직이지 않습니다.
• 커서가 위치한 카드를 뒤집기 위해서는 [Enter] 키를 입력합니다.
  • [Enter] 키를 입력해서 카드를 뒤집었을 때
    • 앞면이 보이는 카드가 1장 뿐이라면 그림을 맞출 수 없으므로 두번째 카드를 뒤집을 때 까지 앞면을 유지합니다.
    • 앞면이 보이는 카드가 2장이 된 경우, 두개의 카드에 그려진 그림이 같으면 해당 카드들이 화면에서 사라지며, 그림이 다르다면 두 카드 모두 뒷면이 보이도록 다시 뒤집힙니다.

"베로니"는 게임 진행 중 카드의 짝을 맞춰 몇 장 제거된 상태에서 카드 앞면의 그림을 알고 있다면, 남은 카드를 모두 제거하는데 필요한 키 조작 횟수의 최솟값을 구해 보려고 합니다. 키 조작 횟수는 방향키와 [Enter] 키를 누르는 동작을 각각 조작 횟수 1로 계산하며, [Ctrl] 키와 방향키를 함께 누르는 동작 또한 조작 횟수 1로 계산합니다.

다음은 카드가 몇 장 제거된 상태의 게임 화면에서 커서를 이동하는 예시입니다.
아래 그림에서 빈 칸은 이미 카드가 제거되어 없어진 칸을 의미하며, 그림이 그려진 칸은 카드 앞 면에 그려진 그림을 나타냅니다.

예시에서 커서는 두번째 행, 첫번째 열 위치에서 시작하였습니다.

[Enter] 입력, ↓ 이동, [Ctrl]+→ 이동, [Enter] 입력 = 키 조작 4회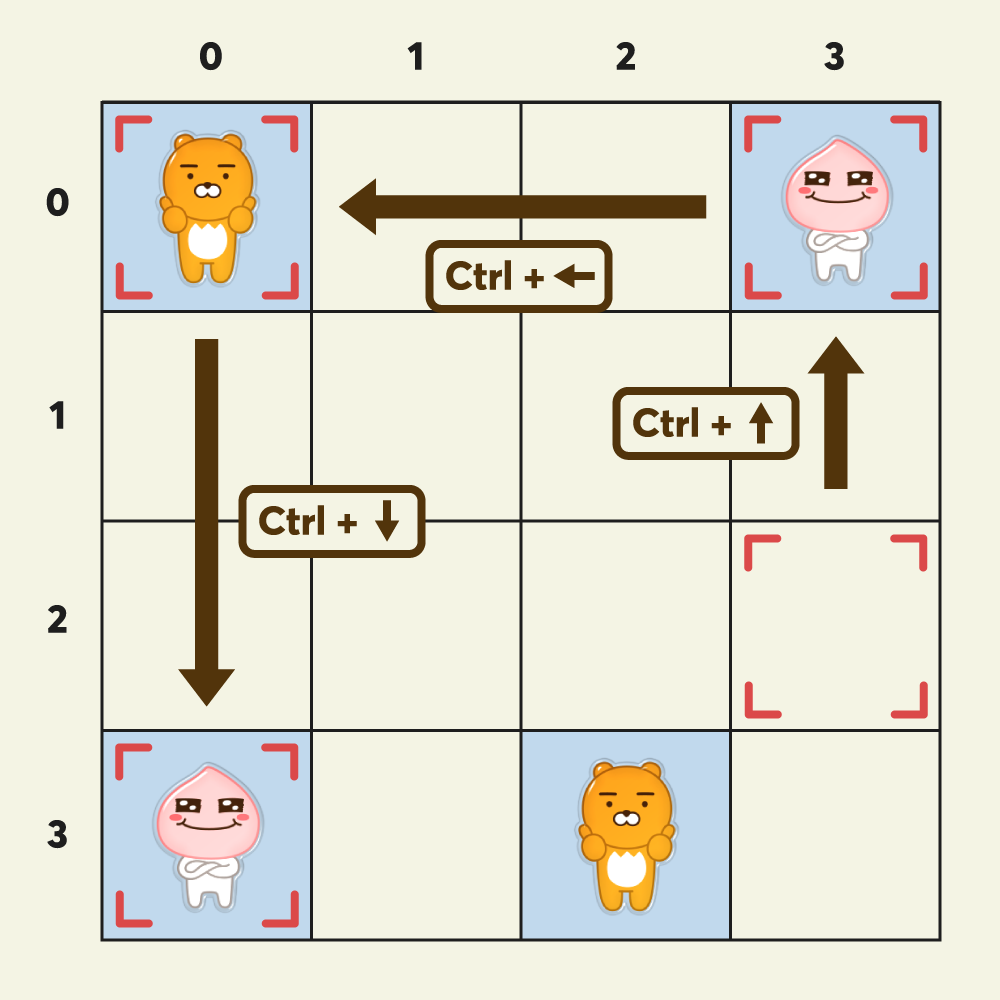

[Ctrl]+↑ 이동, [Enter] 입력, [Ctrl]+← 이동, [Ctrl]+↓ 이동, [Enter] 입력 = 키 조작 5회

[Ctrl]+→ 이동, [Enter] 입력, [Ctrl]+↑ 이동, [Ctrl]+← 이동, [Enter] 입력 = 키 조작 5회

위와 같은 방법으로 커서를 이동하여 카드를 선택하고 그림을 맞추어 카드를 모두 제거하기 위해서는 총 14번(방향 이동 8번, [Enter] 키 입력 6번)의 키 조작 횟수가 필요합니다.

---

[문제]

현재 카드가 놓인 상태를 나타내는 2차원 배열 board와 커서의 처음 위치 r, c가 매개변수로 주어질 때, 모든 카드를 제거하기 위한 키 조작 횟수의 최솟값을 return 하도록 solution 함수를 완성해 주세요.

[제한사항]

• board는 4 x 4 크기의 2차원 배열입니다.
• board 배열의 각 원소는 0 이상 6 이하인 자연수입니다.
  • 0은 카드가 제거된 빈 칸을 나타냅니다.
  • 1 부터 6까지의 자연수는 2개씩 들어있으며 같은 숫자는 같은 그림의 카드를 의미합니다.
  • 뒤집을 카드가 없는 경우(board의 모든 원소가 0인 경우)는 입력으로 주어지지 않습니다.
• r은 커서의 최초 세로(행) 위치를 의미합니다.
• c는 커서의 최초 가로(열) 위치를 의미합니다.
• r과 c는 0 이상 3 이하인 정수입니다.
• 게임 화면의 좌측 상단이 (0, 0), 우측 하단이 (3, 3) 입니다.

---

[입출력 예]boardrcresult

[[1,0,0,3],[2,0,0,0],[0,0,0,2],[3,0,1,0]]	1	0	14
[[3,0,0,2],[0,0,1,0],[0,1,0,0],[2,0,0,3]]	0	1	16

---

풀이

시뮬레이션 + 순열 + bfs 문제였습니다.

우선 순열을 뽑을 카드를 찾습니다. 카드는 1~6의 숫자로 표현됩니다.

//현재 카드 종류를 isNum에 체크해놓고 체크해 둔 숫자중에 순열로 뽑을 예정
for(int i=0; i<4; i++) {
    for(int j=0; j<4; j++) {
        if(board[i][j] == 0 || isNum[board[i][j]]) continue;
        isNum[board[i][j]] = true;
        size++;
    }
}

카드의 종류를 순열을 통해 순서를 나열합니다.(어떠한 순서로 카드를 찾아가야 최소가 될 지 모르기때문에 모든 경우의수를 체크)

//순열로 현재 카드의 방문 순서를 정한다.
public static void Permutation(int cnt, int[] arr, int[][] board, int r, int c) {
    if(size == cnt) {
        //정해진 방문 순서대로 bfs를 돌림
        bfs(board, arr, r, c);
        return;
    }

    for(int i=1; i<=6; i++) {
        if(!isNum[i] || visitedPermutation[i]) continue;
        visitedPermutation[i] = true;
        arr[cnt] = i;
        Permutation(cnt+1, arr, board, r, c);
        visitedPermutation[i] = false;
    }
}

순열로 뽑아졌다면 그 순서대로 bfs를 통해 몇번의 클릭이 필요한지 체크해서 최솟값을 갱신해줍니다.

public static void bfs(int[][] board, int[] arr, int sr, int sc) {
    Queue<Point> q = new LinkedList<>();
    // 최단거리 방문 배열
    boolean[][] visited = new boolean[4][4];
    // 현재 말판을 엔터 쳤는지 체크하는 배열
    boolean[][] boardVisited = new boolean[4][4];
    //최단 거리
    int cnt = 0;
    int answerCnt = 0;
    int idx = 0;
    boolean isSecond = false;

    q.add(new Point(sr, sc));
    visited[sr][sc] = true;

    while(!q.isEmpty()) {
        int len = q.size();

        for(int l=0; l<len; l++) {
            Point now = q.poll();

            if(board[now.x][now.y] == arr[idx] && !boardVisited[now.x][now.y]) {
                //Enter 누적시켜주기
                answerCnt++;
                //지금까지 최소 이동회수 더해주기
                answerCnt+=cnt;
                //이동회수 초기화 -1인 이유는 밑에서 바로 +1을 해주면 0이 되기 때문
                cnt = -1;
                //이미 방문한 말판임을 체크하기
                boardVisited[now.x][now.y] = true;
                //큐 및 visited 비워주기(다시 최단거리로 이동하기 위해)
                q.clear();
                visited = new boolean[4][4];
                //초기 시작점 현재 좌표로 설정
                q.add(new Point(now.x, now.y));
                visited[now.x][now.y] = true;

                //만약 처음 도착한거라면
                if(!isSecond) {
                    //다음엔 두번째임을 체크하기 위함
                    isSecond = true;
                } else {
                    //다음은 새로운 첫번째 말판을 찾아야함을 체크
                    isSecond = false;
                    //다음 말 종류를 찾기위해 순열로 뽑은 배열의 index를 증가시켜줌
                    idx++;
                    //index가 길이보다 길거나 같다 > 즉 모두 다 찾았다.
                    if(idx >= arr.length) {
                        //현재까지 누적한 값의 최소값 찾아줌
                        answer = Math.min(answer, answerCnt);
                        return;
                    }
                }
                break;
            }
            
            //한칸 움직이기
            for(int i=0; i<4; i++) {
                int nx = now.x + dist[i][0];
                int ny = now.y + dist[i][1];

                if(!isIn(nx, ny) || visited[nx][ny]) continue;
                visited[nx][ny] = true;
                q.add(new Point(nx, ny));
            }

            //Ctrl + 움직임
            for(int i=0; i<4; i++) {
                int nx = now.x;
                int ny = now.y;
                
                //범위 끝이면 종료되는 while문
                while(isIn(nx + dist[i][0], ny + dist[i][1])) {
                    nx += dist[i][0];
                    ny += dist[i][1];
                    //만약 엔터치지않은 말이 존재하면 거기에 멈춰짐
                    if(!boardVisited[nx][ny] && board[nx][ny] != 0) break;
                }

                if(!isIn(nx, ny) || visited[nx][ny]) continue;
                visited[nx][ny] = true;
                q.add(new Point(nx, ny));
            }
        }
        cnt++;
    }
}

bfs가 좀 복잡합니다.

일반 bfs와 차이는 2개입니다.

Ctrl + 방향키를 누르는 경우 추가.

만약 카드에 도착해서 Enter를 눌렀다면 그 카드위치부터 다시 출발해야함(초기화를 잘 해주어야했습니다.)

 

전체 코드

package 프로그래머스;

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;

public class PM_카드짝맞추기 {
    static boolean[] isNum, visitedPermutation;
    static int size = 0;
    static int answer;
    static int[][] dist = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};

    static class Point{
        int x;
        int y;

        Point(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }

    public static void main(String[] args) {
        System.out.println(solution(new int[][]{{3, 0, 0, 2}, {0, 0, 1, 0}, {0, 1, 0, 0}, {2, 0, 0, 3}}, 1, 0));
    }

    public static int solution(int[][] board, int r, int c) {
        answer = Integer.MAX_VALUE;
        isNum = new boolean[7];
        visitedPermutation = new boolean[7];

        //현재 카드 종류를 isNum에 체크해놓고 체크해 둔 숫자중에 순열로 뽑을 예정
        for(int i=0; i<4; i++) {
            for(int j=0; j<4; j++) {
                if(board[i][j] == 0 || isNum[board[i][j]]) continue;
                isNum[board[i][j]] = true;
                size++;
            }
        }

        Permutation(0, new int[size], board, r, c);

        return answer;
    }

    public static void bfs(int[][] board, int[] arr, int sr, int sc) {
        Queue<Point> q = new LinkedList<>();
        // 최단거리 방문 배열
        boolean[][] visited = new boolean[4][4];
        // 현재 말판을 엔터 쳤는지 체크하는 배열
        boolean[][] boardVisited = new boolean[4][4];
        //최단 거리
        int cnt = 0;
        int answerCnt = 0;
        int idx = 0;
        boolean isSecond = false;

        q.add(new Point(sr, sc));
        visited[sr][sc] = true;

        while(!q.isEmpty()) {
            int len = q.size();

            for(int l=0; l<len; l++) {
                Point now = q.poll();

                if(board[now.x][now.y] == arr[idx] && !boardVisited[now.x][now.y]) {
                    //Enter 누적시켜주기
                    answerCnt++;
                    //지금까지 최소 이동회수 더해주기
                    answerCnt+=cnt;
                    //이동회수 초기화 -1인 이유는 밑에서 바로 +1을 해주면 0이 되기 때문
                    cnt = -1;
                    //이미 방문한 말판임을 체크하기
                    boardVisited[now.x][now.y] = true;
                    //큐 및 visited 비워주기(다시 최단거리로 이동하기 위해)
                    q.clear();
                    visited = new boolean[4][4];
                    //초기 시작점 현재 좌표로 설정
                    q.add(new Point(now.x, now.y));
                    visited[now.x][now.y] = true;

                    //만약 처음 도착한거라면
                    if(!isSecond) {
                        //다음엔 두번째임을 체크하기 위함
                        isSecond = true;
                    } else {
                        //다음은 새로운 첫번째 말판을 찾아야함을 체크
                        isSecond = false;
                        //다음 말 종류를 찾기위해 순열로 뽑은 배열의 index를 증가시켜줌
                        idx++;
                        //index가 길이보다 길거나 같다 > 즉 모두 다 찾았다.
                        if(idx >= arr.length) {
                            //현재까지 누적한 값의 최소값 찾아줌
                            answer = Math.min(answer, answerCnt);
                            return;
                        }
                    }
                    break;
                }
                
                //한칸 움직이기
                for(int i=0; i<4; i++) {
                    int nx = now.x + dist[i][0];
                    int ny = now.y + dist[i][1];

                    if(!isIn(nx, ny) || visited[nx][ny]) continue;
                    visited[nx][ny] = true;
                    q.add(new Point(nx, ny));
                }

                //Ctrl + 움직임
                for(int i=0; i<4; i++) {
                    int nx = now.x;
                    int ny = now.y;
                    
                    //범위 끝이면 종료되는 while문
                    while(isIn(nx + dist[i][0], ny + dist[i][1])) {
                        nx += dist[i][0];
                        ny += dist[i][1];
                        //만약 엔터치지않은 말이 존재하면 거기에 멈춰짐
                        if(!boardVisited[nx][ny] && board[nx][ny] != 0) break;
                    }

                    if(!isIn(nx, ny) || visited[nx][ny]) continue;
                    visited[nx][ny] = true;
                    q.add(new Point(nx, ny));
                }
            }
            cnt++;
        }
    }

    public static boolean isIn(int x, int y) {
        return 0<=x && x<4 && 0<=y && y<4;
    }

    //순열로 현재 카드의 방문 순서를 정한다.
    public static void Permutation(int cnt, int[] arr, int[][] board, int r, int c) {
        if(size == cnt) {
            //정해진 방문 순서대로 bfs를 돌림
            bfs(board, arr, r, c);
            return;
        }

        for(int i=1; i<=6; i++) {
            if(!isNum[i] || visitedPermutation[i]) continue;
            visitedPermutation[i] = true;
            arr[cnt] = i;
            Permutation(cnt+1, arr, board, r, c);
            visitedPermutation[i] = false;
        }
    }
}